【自著論文を解説】Supervised STDP Learning with Weight Decay for Spiking Neural Networks
論文が公開されました!
大学院を修了して3年ほど経ちますが、最近私の修士研究がICOIACT 2023という国際学会で発表され、先日IEEEでも公開されました。
日本語タイトルは「スパイキングニューラルネットワークのための重み減衰付き教師ありSTDP学習」です。
ちょっとした自慢ですが、ICOIACTでBest paperとして選出されました! (2/93件)
自著論文を解説してみる
ということで、公開されてだいぶ経ってしまいましたが、自分で書いた論文を解説します。
全て細かく解説すると、論文の意を為さない気がするので、わかりにくいポイントをかいつまんで補足する形にします。
なので、上記論文と併せて読んでいただけると理解が深まりますので、ぜひ興味を持たれ方は上記論文を手元にご用意いただけると幸いです。
便宜上、スパイキングニューラルネットワークをSNN、それ以外の昨今よく使われているニューラルネットワークをANNと表記します。
SNNの基礎知識などは、私著の下記ページも参考にしてください。
ゼロから学ぶスパイキングニューラルネットワーク- Spiking Neural Networks from Scratch (snn.hiral.net)
Summary (この論文は何を言っているのか)
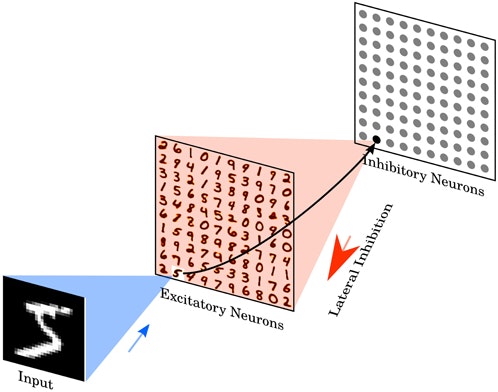
この論文はDieal & Cookモデルという、有名なSNNのための教師なし学習方法をベースとしています。
Dieal & CookモデルはSTDP (Spike-timing-dependent plasticity: スパイクタイミング依存可塑性) 学習則 というニューロン間の生物学的な性質を実際の工学的モデルに落とし込み、教師なしで学習させる手法を編み出しました。
※ STDP学習則はあとで補足します
この手法では、MNISTと呼ばれる28×28の白黒手書き数字をターゲットとしており、昨今の人工知能モデルからすると、「なんだそれだけかよ」と思うかもしれませんが、SNNではまだ強力な学習方法が確立されておらず、しかも生物学的に妥当性のある学習方法を使ったモデルということで、素晴らしい研究成果です。
しかし、このDieal & Cookモデルにもいくつか欠点や課題があります。
それを解消すべく、STDP学習則を使いつつ、より別のアプローチでより良い学習方法を提案した、というのがこの論文の核となります。
余談: 誤差逆伝播学習法 (Back Propagation) と SNN
昨今のニューラルネットワークモデルでは、誤差逆伝播学習法と呼ばれる、かなり強力な学習方法がありますね。
誤差を前ニューロン層に伝播させて、誤差を小さくしていく画期的な学習方法ですが、これはSNNにはそのまま適用できません。
誤差逆伝播学習法は、ReLUやシグモイド関数をはじめとする、勾配を算出できる非離散的な活性化関数を使っているモデルにしか適用不可能です。
したがって、もともとスパイク列という離散的な情報を扱うSNNにはそのまま適用は難しいです。
Spike-propという誤差逆伝播学習法のアプローチをうまくSNNに当てはめてみた学習法もありますが、やはりANNにはまだ勝てず、「そもそも生物学的により妥当なSNNというモデルを使っておきながら、生物学的に無理がある誤差逆伝播学習法を使うのか?」という意見もあるでしょう。
SpikeProp: backpropagation for networks of spiking neurons. (Sander M. Bohte et al., 2000)
私はこの「生物学的に無理がある誤差逆伝播学習法を使わずに、STDPなどの学習則をうまく利用したい」という考えを尊重していて、誤差逆伝播学習法を真似るという方向性を否定したいわけではないですが、SNNにはSNNに合った別の学習手法があるはず、と考えています。
Dieal & Cookモデルについて
まずは先行研究の課題を整理します。
これを理解しないと、私の提案手法へのアプローチの理解が難しいです。
Dieal & Cookモデルは、教師なし学習であることが大きな特徴ですが、識別器として扱う上では少し工夫が必要です。
学習自体は下記Gifのように、勝手に出力層ニューロンが自分の役割を適宜決めて重みを学習していきます。
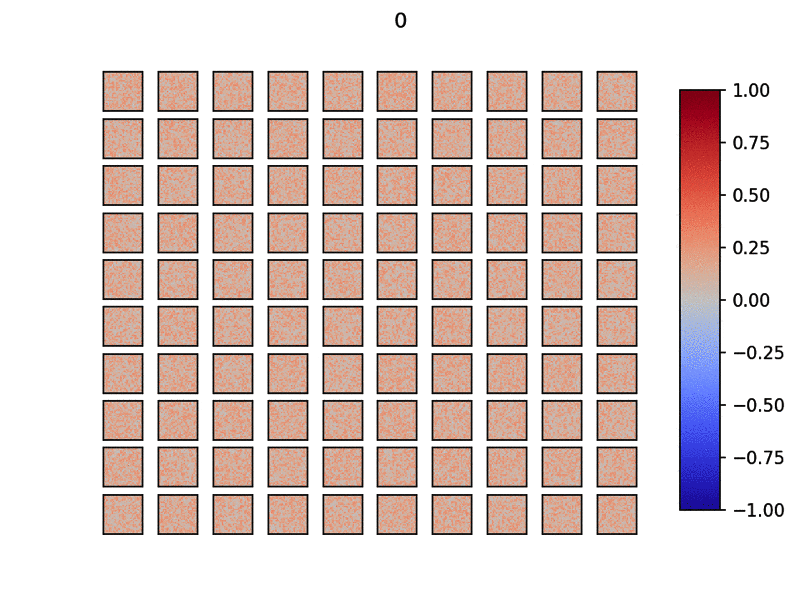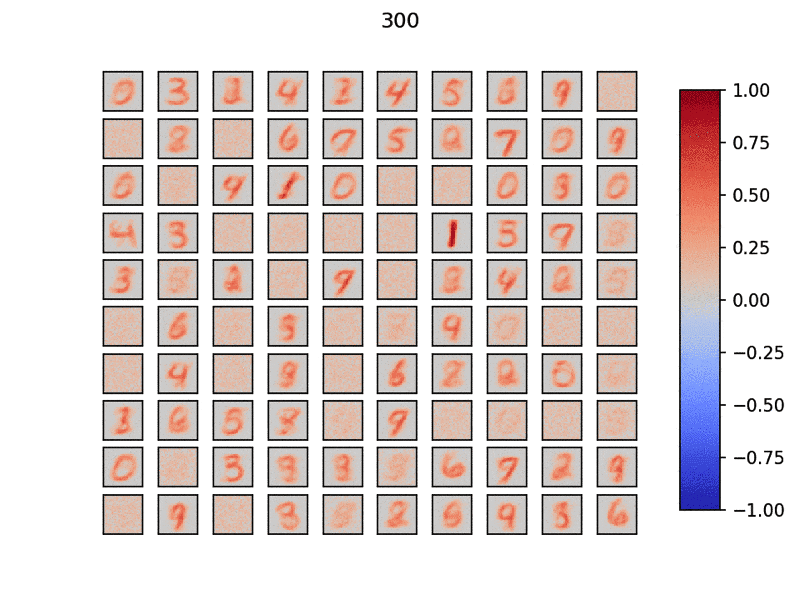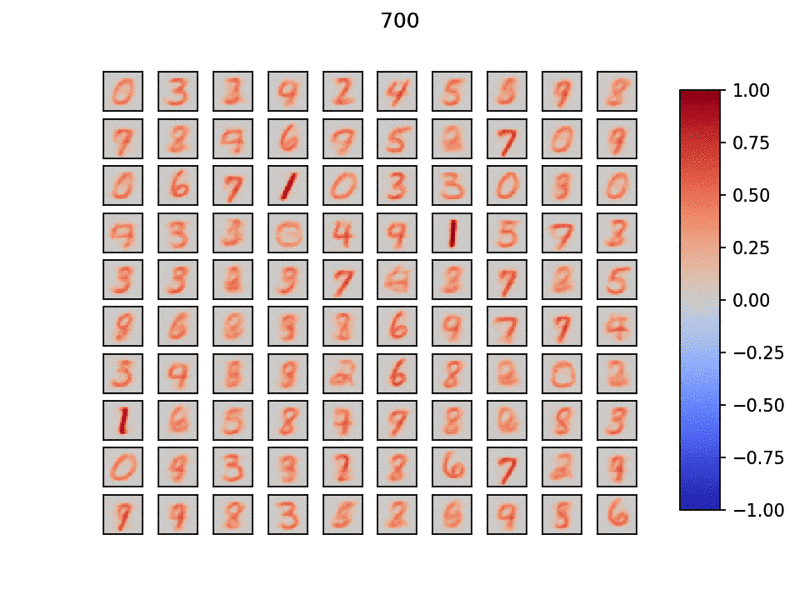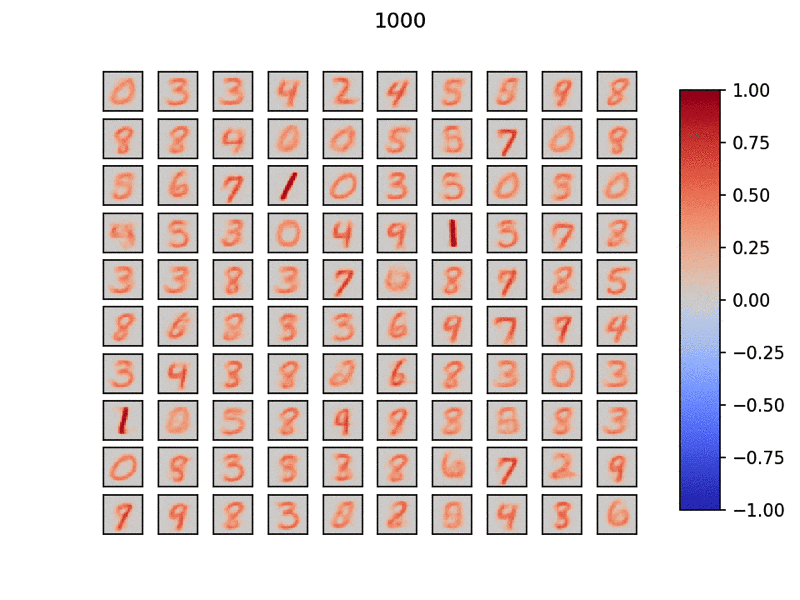
学習後は、再度学習データを流し、一番反応が良いニューロンに対してその入力データに紐づくラベルを割り当てていきます。
なので、学習自体は教師なしですが、最終的に識別器として扱うには、入力データのラベルを用いることになります。
結局教師ラベルを使うことになるので、学習時にもラベル使って教師あり学習にしても良いのでは? と考える方もいるでしょうが、学習自体は教師なしなので、画期的で生物に近そうな学習法です。
では、なぜ各出力層ニューロンは勝手にデータをたくさん重複することなく学習できているのでしょうか?
ここがこの研究の肝であり、課題でもあります。
この学習を成り立たせている要素は4つあります。
- STDP学習則
- 側抑制
- 重みの正規化
- 動的に変化する発火閾値
STDP学習則
STDP学習則は局所的に起こるニューロン間のシナプス結合荷重を変化させる生物学的現象です。
かの有名な Hebb則より精緻な学習則とも言われており、生物学的に妥当性のある学習則と言えます。
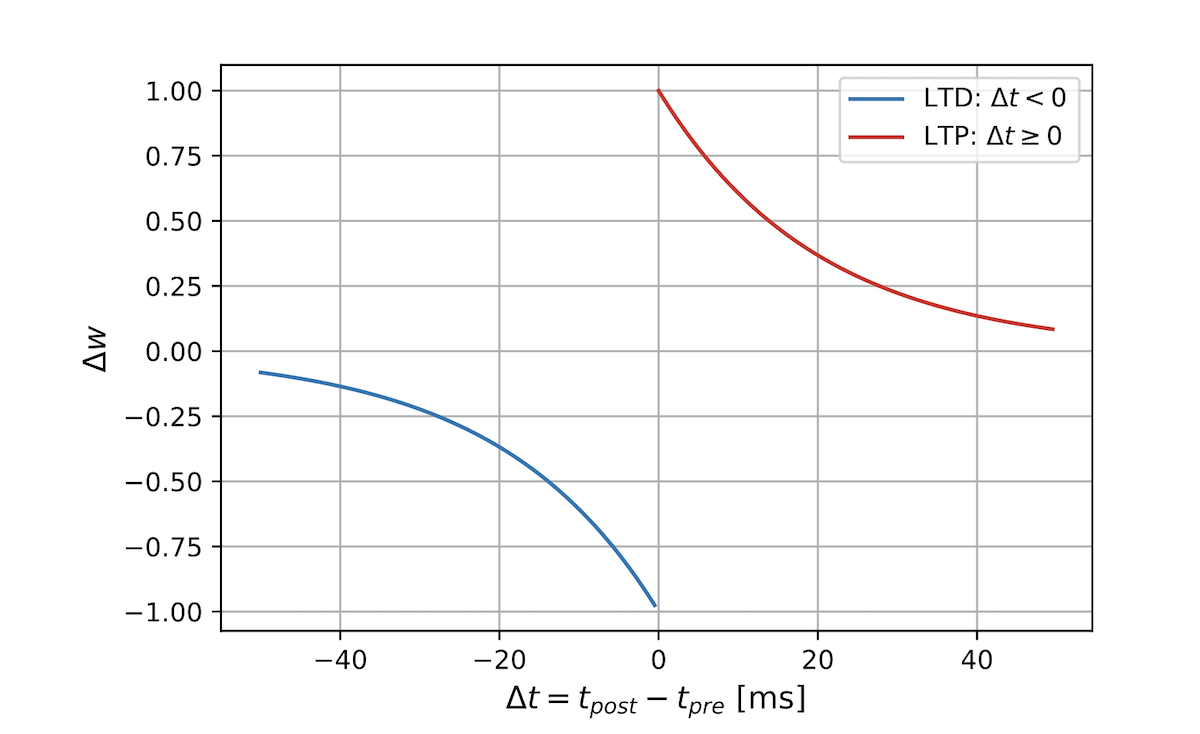
STDP学習則にもいくつか種類があるのですが、今回はメジャーな下記のような式を用いています。
\(\begin{equation}\
\Delta w =
\left\{
\begin{array}{l}
A_{+}exp(\Delta t / \tau_{+}),\ \ \ if \ \ \ \Delta t \geq 0\\
A_{-}exp(\Delta t / \tau_{-}),\ \ \ if \ \ \ \Delta t < 0
\end{array}
\right.
\end{equation}\)
ここで \(t_{pre}\) および \(t_{post}\) はそれぞれ前/後ニューロンのスパイク発火時刻です。
つまり、前後ニューロンの発火時刻が近ければ近いほど重みの更新量は大きくなっていくようなイメージです。
言い換えると、前ニューロンの発火に起因して後ニューロンが発火したと思われる場合には、重みは強くなります。
もちろんニューロン間の結合は1対1ではなく、多対多なので、関係性が大きいと思われるニューロン間の重みが強くなるイメージです。
これがDiel & Cookモデルの学習の核となりますが、前述したようにこれだけでは学習はできません。
側抑制
いわゆるWinner-take-allサーキットや先勝ち回路のようなイメージで、最初に発火した出力層ニューロンは、他の出力層ニューロンの発火を抑制するような形になっています。
出力層ニューロン同士は強い負の重みで相互結合しており、ある出力層ニューロンが発火すると、それ以外の出力層ニューロンは強い抑制を受けて発火しなくなるようになるので、これにより出力層ニューロンの学習するデータにバリエーションがでてきます。
重みの正規化
これは外部から適用しているもので、やや人為的な操作です。
STDP学習則によって学習したニューロンは似たデータが来ると、どんどん重みが強化されていき、正の方向に発散していきます。
それを抑制するために、入力層ニューロンから出力層ニューロンへつながる重みを均していくのが、重みの正規化です。
\(\|{\mathbf{w}}\| \leq dim \ {{\mathbf{w}}/10}\)
という式で正規化されていきます。
ここで\(\|{\mathbf{w}}\|\) はL1ノルムで、Dieal&Cookモデルでは入力層ニューロンは28×28=784個あり、出力層ニューロンへの重みの数も 784 になるので、実際には \(\|{\mathbf{w}}\| \leq 78.4\) という正規化がなされます。
動的に変化する発火閾値
Adaptive thresholdと表記しているものです。
このDieal&Cookモデルでは、LIF (Leaky integrated and fire) モデルというニューロンモデルを用いているのですが、発火閾値の扱いが少しだけアレンジされています。
LIFモデルの膜電位 \(V(t)\) は、下記の微分方程式によって定ります。
\(\tau_{m}\frac{dV(t)}{dt}=(-V(t) + E_{rest}) + I(t)\)
この \(V(t)\) が発火閾値 \(V_{\theta}\) を超えた時に、ニューロンは発火しますが、この\(V_{\theta}\)は固定値ではなく、動的に変化させる方式をとっています。
\(V_{\theta} = \theta_{0} + \theta(t)\)
\(\theta(t) \leftarrow \theta(t) + \alpha_{\theta}s(t)\)
\(\tau_{\theta}\frac{d\theta(t)}{dt} = -\theta(t)\)
上記の式によって、発火閾値\(V_{\theta}\)は決定します。
ここで、\(\tau_{\theta}\)は時定数、\(\theta_{0}\)は初期発火閾値、\(\alpha_{\theta}\)は上昇係数です。
したがって、発火閾値はニューロンが発火すると、\(\alpha_{\theta}\)だけ上昇し、時間とともに時定数に依存して減衰していくような形をとります。
これにより、ある程度学習を終えたニューロンは発火しにくくなり、他のニューロンへ学習機会を提供することができます。
ちなみに、入力電流 \(I(t)\) については、3-5. 入力電流の計算 – ゼロから学ぶスパイキングニューラルネットワーク をご参照ください。ここでは割愛します。
Dieal & Cookモデルの課題は何か
一見、よくできたモデルなのですが何が課題なのでしょうか?
まずは、上記の4つの要素のうち、動的閾値と側抑制をなくしたら、どうなるか見てみます。
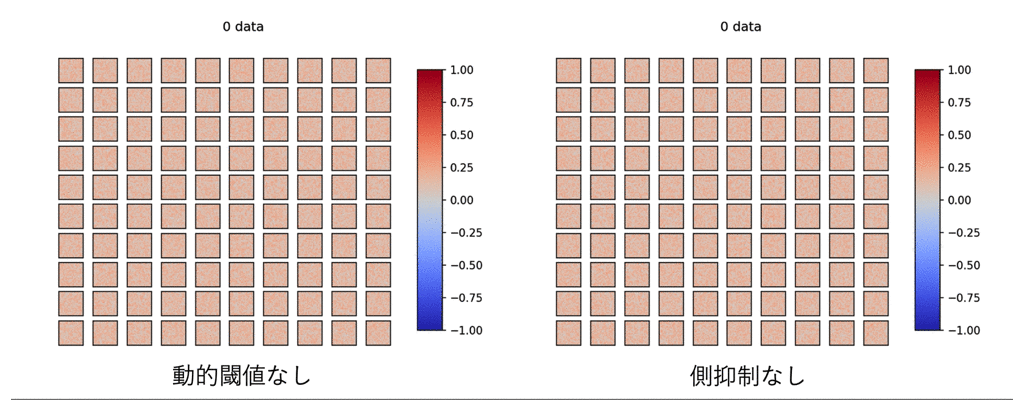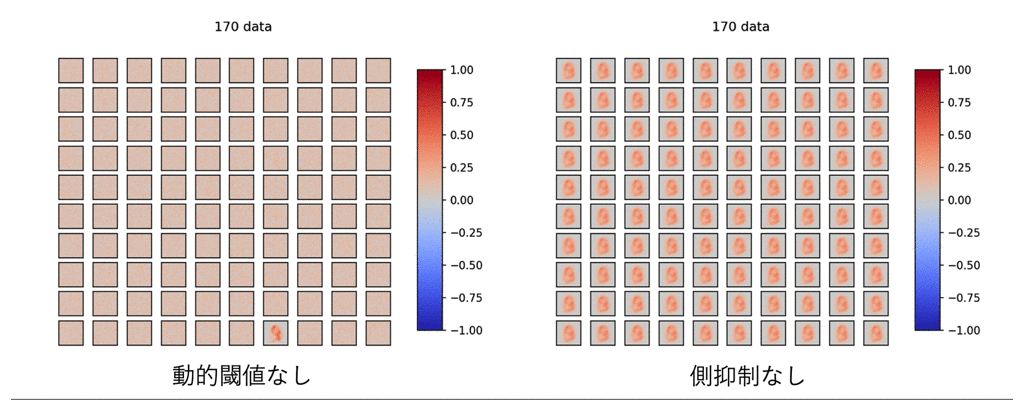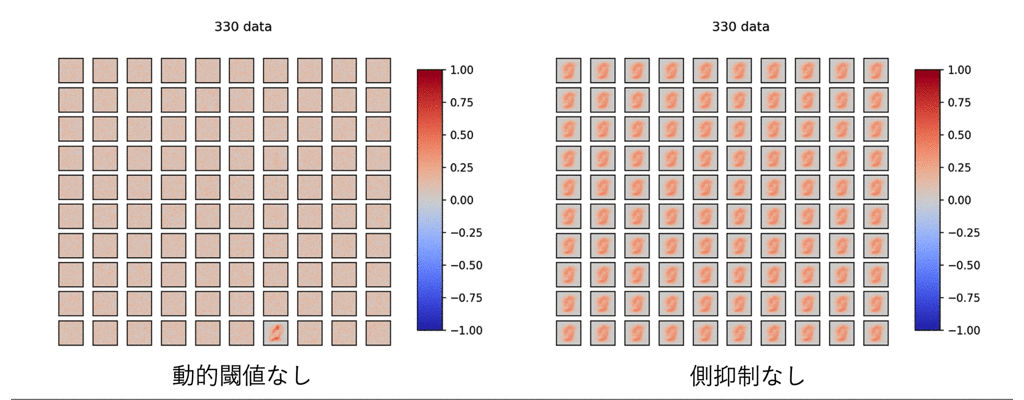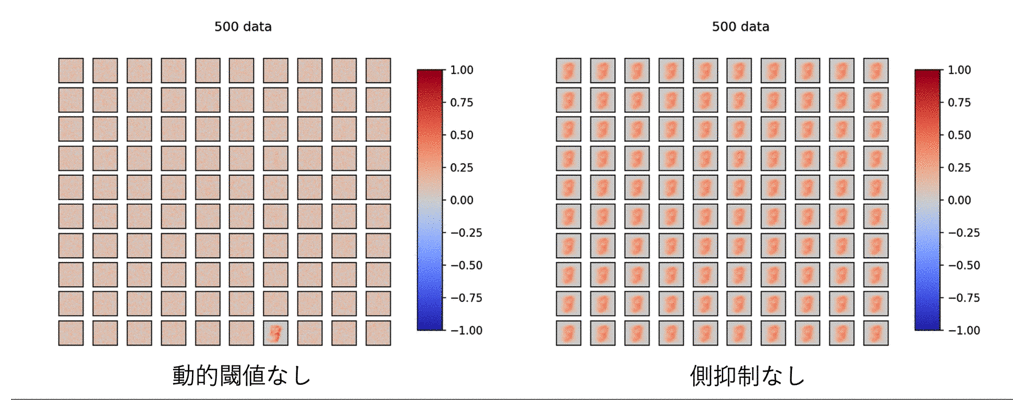
ご覧の有様です。
これを見ると、この2つの学習への寄与が偉大なものであることを物語っています。
よく見ると、このDieal&Cookモデルではほとんど正の重みで構築され、効率的に重みを扱えていないことも伺えます。
このモデルでは出力層ニューロンも6400個ものノードを用いており、学習がやや非効率であることが伺えます。
2つ目の課題としては破局的忘却 (Catastrophic Forgetting) です。
これは、ANNでもよくある話なのですが、こういったモデルは入力データをランダムに与えることが前提であり、1 → 2 → 3… と順番にデータを与えていくと最初に学習したデータを忘却してしまい、継続的な学習ができないことを破局的忘却と言います。
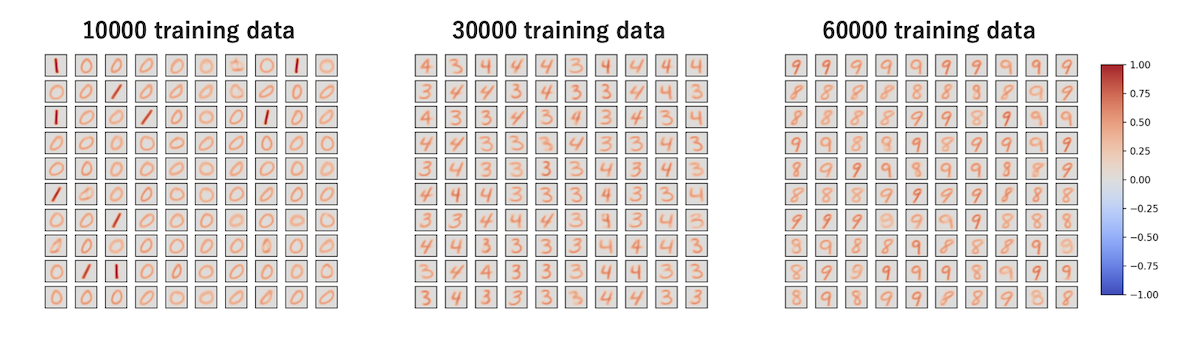
上記はMNISTを1のラベルから順に学習させた場合で、全データを学習し終えた段階では、8や9しか覚えていません。
これも、私の提案手法における1つの課題としています。
最後に、データのラベルの使い方も課題だと感じており、識別器として扱うためにどうせラベルを使うのであれば、学習時点で利用してもっと効率的に学習できないか、と考えました。
まとめると、私が解消したいのは、
- データに対して巨大なモデルであり、学習効率がやや悪い
- 破局的忘却の抑止
- 学習データのラベルをうまくつかって効率よく学習させたい
じゃあどうアプローチするか
私のアイデアは、「STDP学習則は前後ニューロンが近い時間で発火したら学習される」ことからきており、「学習させたいニューロン以外には黙っててもらう」です。
通常の教師あり学習というと、出力層ニューロンにあらかじめ役割 (ラベル) を割り当てておいて、そのニューロンは出力を1に、それ以外は0に近づけていく、というものです。
私の提案手法では、「役割ではないニューロンだけ発火をさせない」というものでやや異なります。
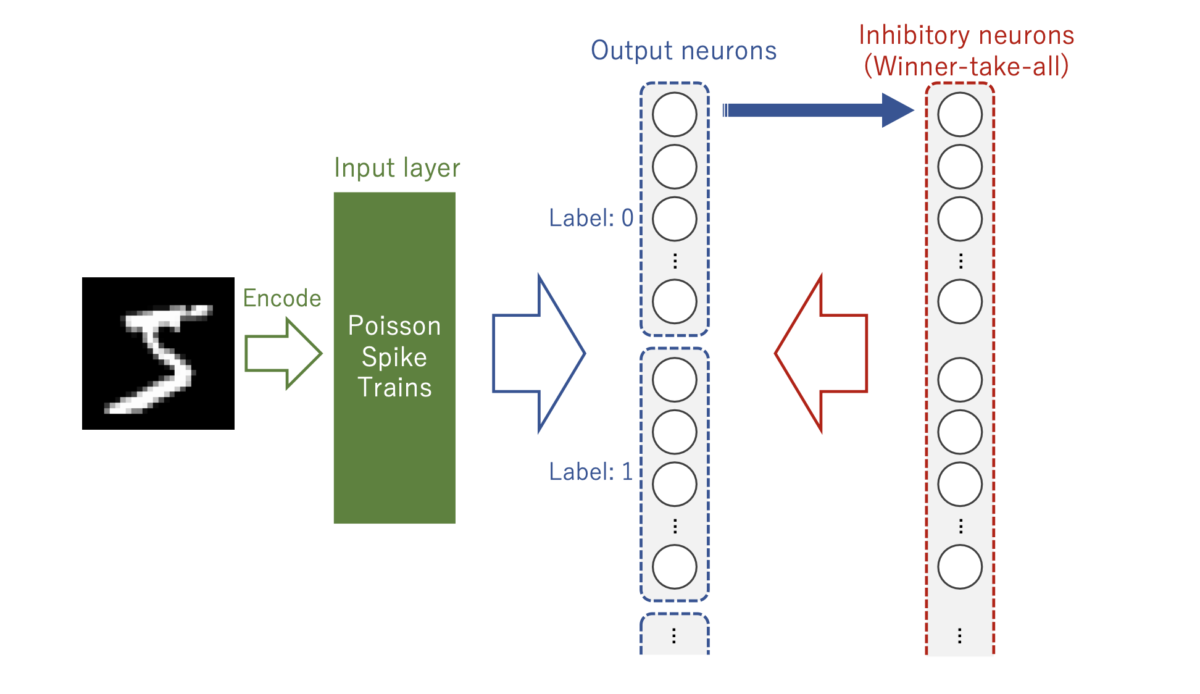
ネットワーク構成はDieal&Cookモデルと大差はありませんが、出力層ニューロンには役割を与えています。
1つのニューロンに1つのラベル、というわけではなくある程度グループでわけ、覚えるデータのばらつきを許容できるようにしています。
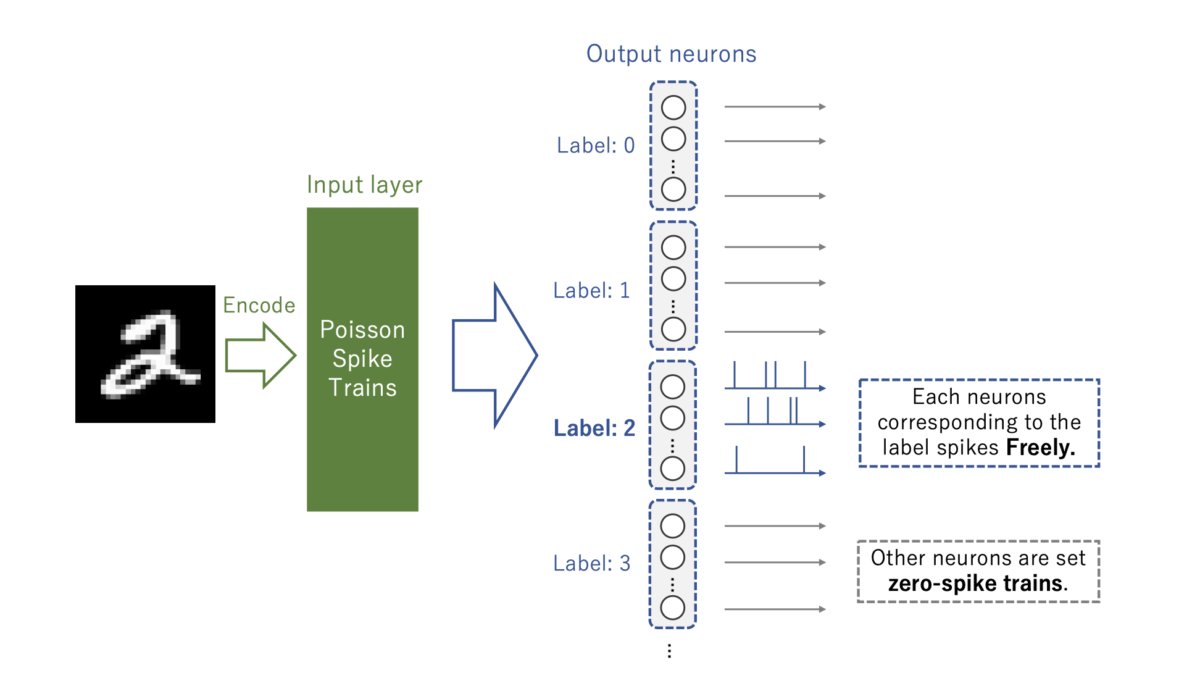
学習については、先に述べたように 対象のニューロンには自由に発火してもらい、それ以外はスパイク無しの出力として抑制させます。
何度も言っていますが、STDP学習則は2つのニューロンが発火して適用される学習則です。
したがって、学習させる重みを限定させることができます。
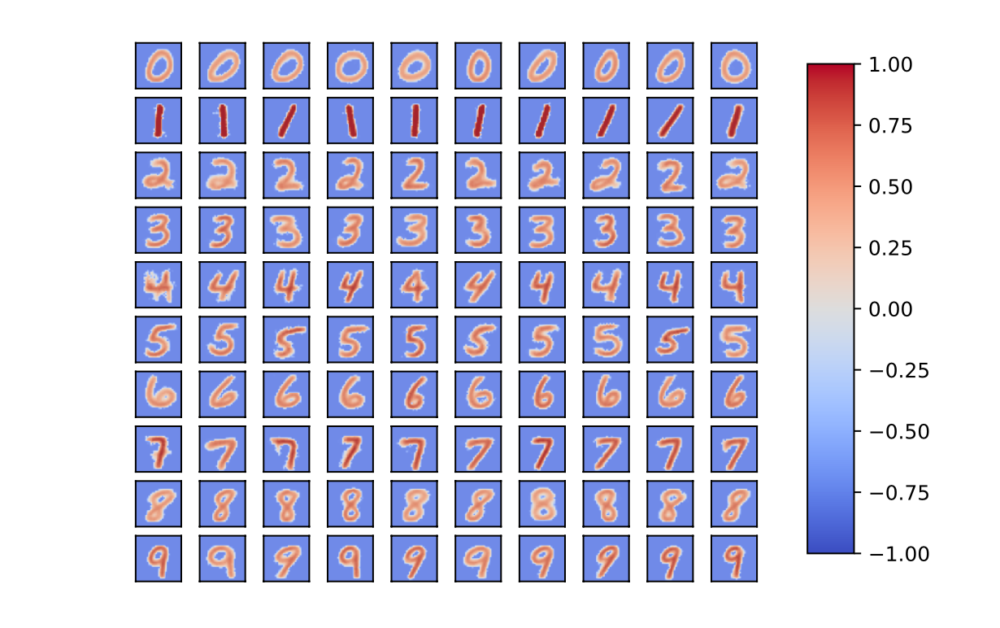
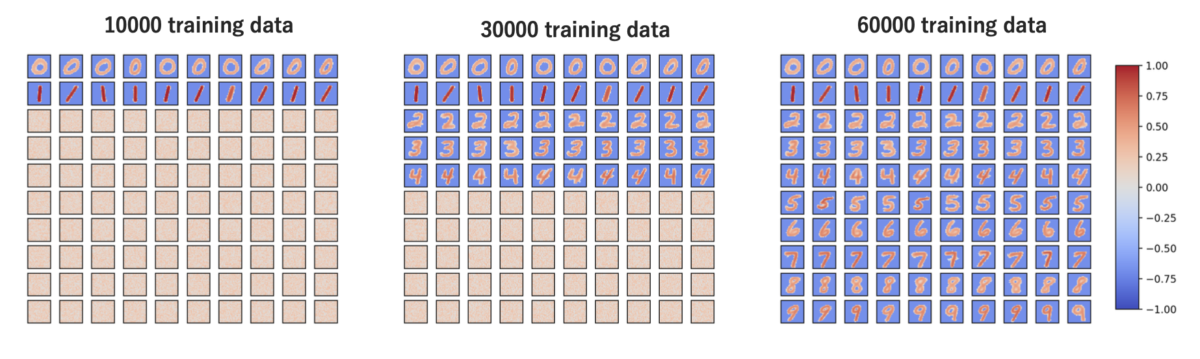
これによって下記のような重みが学習できます。
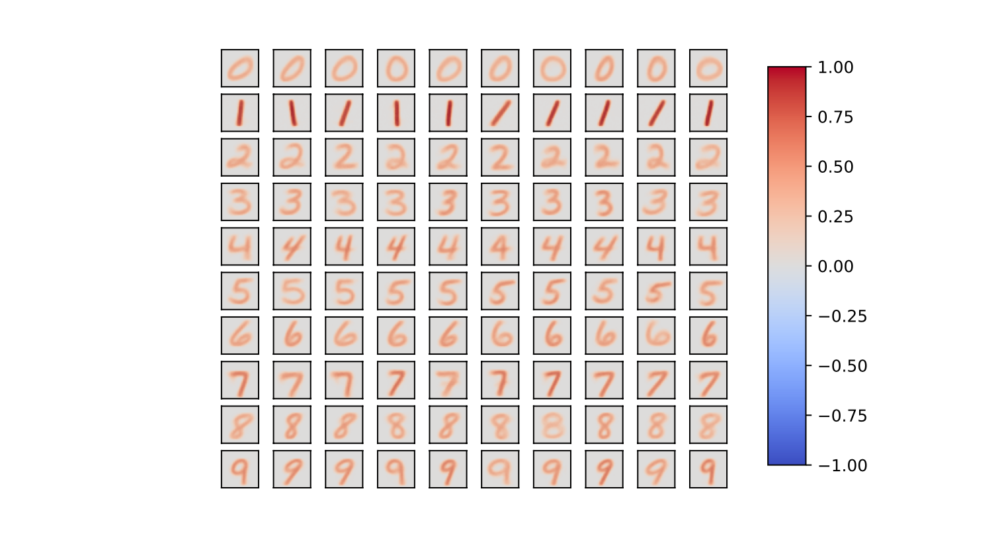
例として各ラベル10ニューロンで計100個の出力層ニューロンを用意してみましたが、綺麗に学習分けができています。
ここまでは、Dieal&Cookモデルと結果に大差はありません。
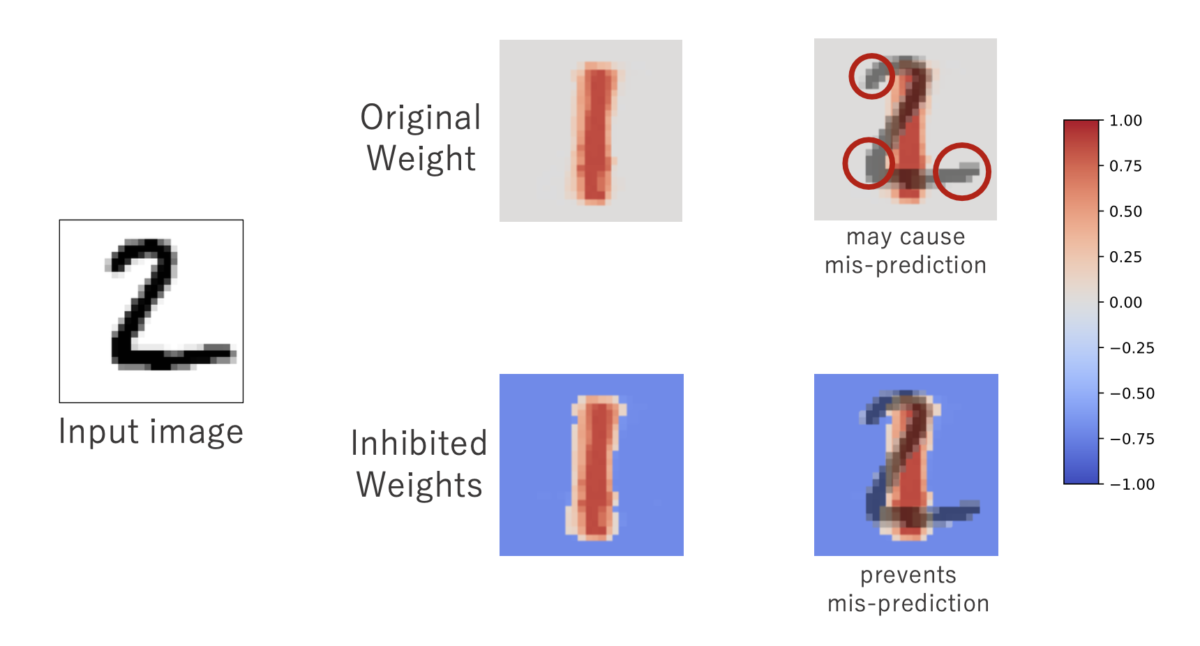
次に注目すべきは、負の重みがなく効率よく識別ができていない点です。
重みの正規化により、文字の占有面積が小さなデータ (例えば 1) ほど、大きな正の重みが集まりやすいために、誤識別を起こしてしまいます。
下記の図はICOIACTの論文には非掲載ですが、横軸が時間で青いプロットが発火時刻 (=スパイク) だと思ってください。
縦軸には100個の出力層ニューロンが10個ごとにラベルでグルーピングされている様を表しています。
たくさん発火しているニューロンのラベルが識別結果となります。
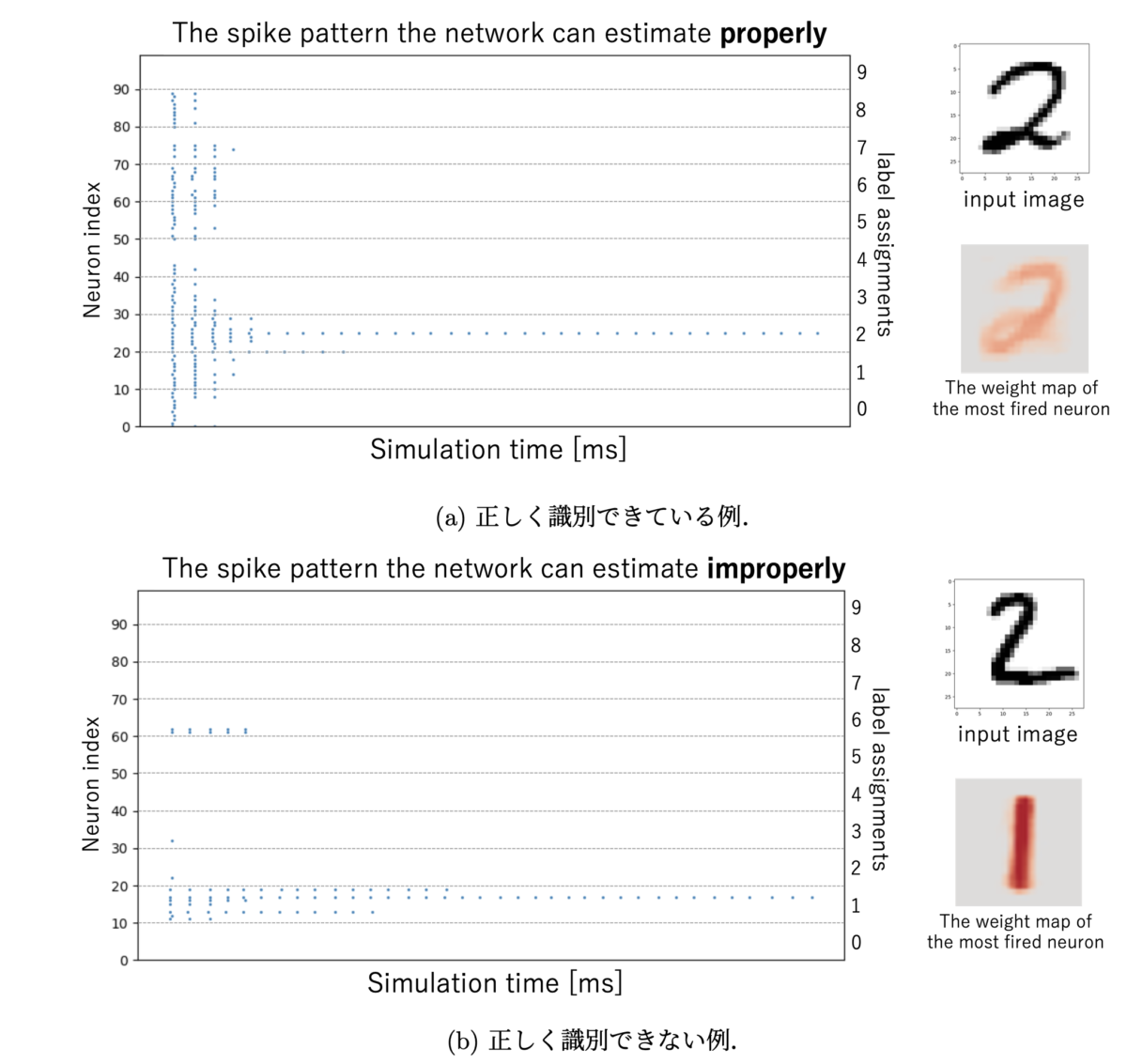
負の重みがないゆえに、(b) では “1” と誤識別を引き越してしまっています。
そこで、重みの正規化に工夫を加えます。
\(\tau_{w}\frac{dw}{dt}=(-w + W_{inh})\cdot s(t)\)
\(\tau_{w} = \frac{\tau_{w_{0}}}{\exp(\alpha(w+\beta))}\)
ここで、\(W_{inh}\)は重みの収束定数で、\(\tau_{w_{0}}\)は時定数、\(\alpha, \beta\)は減衰係数です。
これが重み減衰 (Weight Decay) 機構です。
これにより、下記のように負の重みを自動的に獲得することができ、誤識別率をグッと下げることができました。
結果
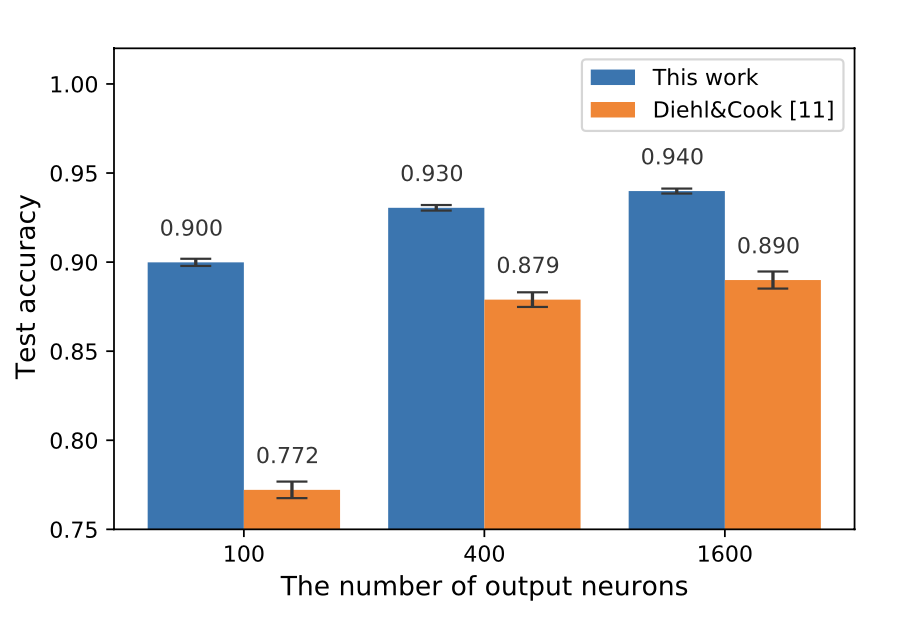
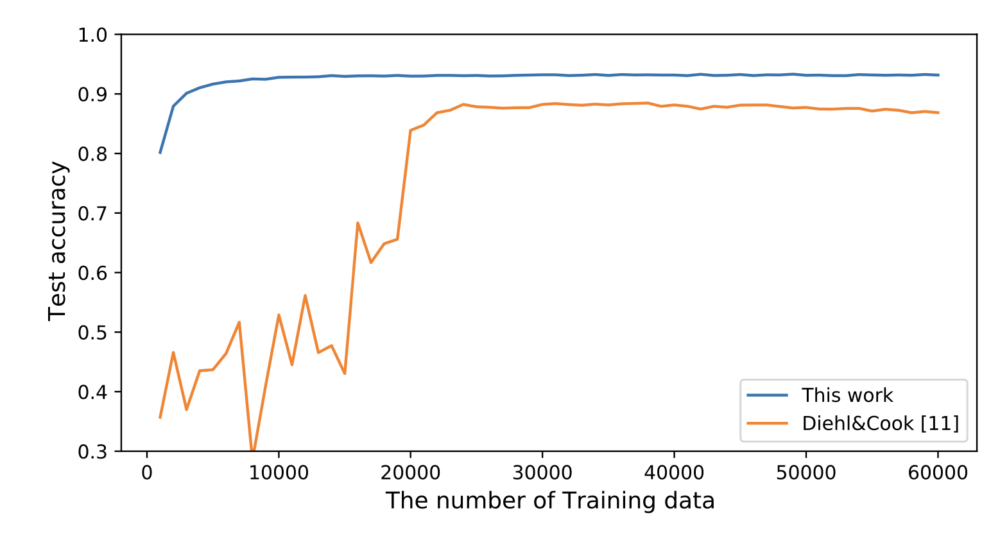
結果は論文に記載していますので、そちらを参照していただきたいのですが、学習収束も早く、学習のために必要なニューロン数を少ないモデルで、良い識別制度を獲得できました。
また、破局的忘却に関してはこの学習方法では無縁と言って良いので、もちろん引き起こしません。
課題と展望
散々 “生物学的妥当性のある学習法” 云々言っていましたが、結局STDP学習則だけではなく、重み減衰や側抑制などのメカニズムはDieal&Cookモデルを踏襲した形になったので、ここにはまだ課題があります。
STDP学習則はあくまで局所的な学習則なので、全体を見る何かしらのメカニズムは必要になってしまうのですが、そのメカニズムをより生物学的妥当性のあるものに代替できるとなお価値ある学習方法になったと思います。
また、まだ小さなデータでしか学習ができていないので、より大きな学習データを学習できるようにしたり、CNN (Convolution NN) のような画像を効率よく直腸抽出できる多層ネットワークへの拡張も大きな課題です。
さいごに
ざっくりな紹介・解説になりましたが、論文を読むのはなかなか大変な作業ですので、少しでも理解の手助けとなったら嬉しいなと思ってこの記事を書くに至りました。
私の論文はある程度評価いただいているのですが、まだまだ課題はあって、理想には程遠いので、もっともっと多くの人にSNNの研究に取り組んでもらい発展させていってほしいです。
もしご質問等あれば、お気軽にお問い合わせください。
最後までご精読ありがとうございました!